Mechanics
Energy
Potential (stored) energy, due to gravity or an energy store Kinetic energy, due to a linear or angular velocity
Energy in a closed system must be conserved
Some energy forms are
- magnetic (flux and magnetic intensity)
- mechanical - kinetic
- thermal - heat
- light (EM waves)
- gravitational potential
- chemical - chemical bonds
- sound - pressure and velocity
- electrical (voltage and current)
- elastic potential
- nuclear (mass to energy exchange)
Mechanisms to dissipate energy
- Heat
- Sound
- Light
- Chemical reaction
- Any others?
efforts (force)
- force
- torque
- shear
- pressure
- stress
flows (velocity)
- position, velocity, acceleration
- angular speed, angular acceleration
- strain, deflection
Centre of mass, momentum and moment of inertia (vector forms)
Please familiarise yourself with the concept of centre of mass (see youtube links below)
Newton's equation
Applies to forces acting on a point coincident with the centre of mass of an object
\[ \sum\vec{f}=m\vec{a} \]Question does the object respond to the force or the acceleration?
Newton's equation can also be considered as the force causing a change in momentum, that is
\[f=\frac{d\vec{p}}{dt}\]where $\vec{p}=mv$ is the momentum (mass $\times$ velocity) of the object.
- Mass $m$ is a (scalar) property of an object in space and dictates the acceleration of that object when a force $\vec{f}$ is applied.
- Momentum ($\vec{p}$) can be expressed as a vector and is a conserved property leading to Noether's idea of translational invariance.
- Weight is a property of an object in a gravitational field. If that object is not moving then the Weight relates to the force that the gravitational field applies to the mass.
Newton-Euler's equation
N-E applies when considering an object responding to a torque by spinning.
\begin{equation} \sum{\vec\tau}=J\dot{\vec\omega}+\vec\omega \times J\vec{\omega}\label{eq:NE} \end{equation}where $\tau$ is a torque and $\omega$ is an angular velocity.
Also
- Moment of inertia $J$ (or sometimes $I$) is a (matrix) property of an object that relates to spinning and dictates the angular acceleration $\dot{\vec\omega}$ of that object when a torque $\vec\tau$ is applied.
- Angular momentum $L$(or moment of momentum), is $J\vec\omega$.
A special case applies when an object is spinning around its centre of mass. In this case $J$ is a diagonal matrix, so the term $\vec\omega \times J\vec{\omega}$ vanishes (angle between vectors is 0 hence cross product is 0).
Newton-Eulers equation parallels Newtons equation for linear momentum so $\sum\vec\tau=\frac{d L}{dt}$
Conserved quantities (Noether's first theorem)
Noether's theorem - named after Emmy Noether - relates conserved quantities to invariance[banados16:_noeth]. See (https://www.discovermagazine.com/the-sciences/how-mathematician-emmy-noethers-theorem-changed-physics)
| continuous symmetry | continuity |
| time (experiments that give the same result today as yesterday) | Conservation of energy/mass |
| space (things happen the same in different places) | Conservation of momentum |
| orientation (ditto orientation) | Conservation of angular momentum |
| wave function/Gauge invariance (e.g. light is the same everywhere) | Conservation of electric charge |
| A consequence of energy conservation is system time invariant. That is an identical system will behave the same way at different points in time. |
| A consequence of linear momentum conservation is spatial invariant. That is an identical system will behave the same way at different positions in space. |
| A consequence of angular momentum conservation is orientation invariant. That is an identical system will behave the same way at different orientations in space. |
| Common symbol | relationships | |
| Energy | $E$ | $\frac12 m v^2$ (KE), $\frac12Kx^2$ (PE spring), $mgh$ (PE mass) |
| Linear momentum | $p$ | $f=\frac{d p}{dt}$ |
| Angular momentum | $L$ | $\vec{L}=J\vec\omega=\vec{r}\times \vec{p}$ $\tau=\frac{dL}{dt}$ |
Example of conservation of energy and angular momentum
Vector revision
Much of this lecture will be in standard engineering maths books such as Stroud[Stroud13]
Vectors
A vector $\vec{f}$ is an ordered sequence of $n$ numbers. These numbers can be real in which case $\vec{f}\in\mathbb{R}^n$ or complex numbers where $\vec{f}\in\mathbb{C}^n$. A vector has a magnitude and a direction so it can be considered to represented as an arrow in $n$ dimensions.
One way to consider the array of numbers representing a vector is as an $n\times1$ column matrix ($n$ rows 1 column). For example a vector representing a point in space could be written as $\vec{f}=\begin{bmatrix}1&2&3\end{bmatrix}^T$
An inner and an outer product between two vectors can be defined.
dot product (inner product)
The dot product of two vectors, or a vector with itself requires the vectors have the same number of elements and results in a scalar value.
- If the vector is defined as a column matrix $\vec{a}^T=\begin{bmatrix}a_1&a_2&\dots\end{bmatrix}$ then the dot product $\vec{a}\cdot\vec{r}=\vec{a}^T\vec{r}$
- If the vector is defined as a set of values $\vec{f}=(f_1,\, f_2,\, \dots\, f_n)$ then the dot product $\vec{f}\cdot\vec{r}=\sum_i^n f_i r_i$
- If the angle between two vectors is $\theta$ the dot product is $\vec{f}\cdot\vec{r}=|\vec{f}|\,|\vec{r}|\cos\theta$
if $\vec{r}$ is a basis vector for a coordinate frame (see below) then the dot product of $\vec{f}\cdot\vec{r}$ is the component of $\vec{f}$ along the axis that has $\vec{r}$ as its basis vector.
The dot product is commutative i.e. $\vec{a}\cdot\vec{r}=\vec{r}\cdot\vec{a}$
The magnitude of a matrix can be calculated from the dot product. That is $|\vec{f}|=\sqrt{(\vec{f}\cdot\vec{f})}$ or if the vector is considered as a 1 column matrix, $|\vec{f}|=\sqrt{(\vec{f}^T\vec{f})}$
cross product (outer product)
The cross product of two vectors, or a vector with itself requires both vectors to be in $\mathbb{R}^3$ and results in a vector also in $\mathbb{R}^3$ . The cross product is not commutative (so $\vec{f}\times\vec{r} \ne \vec{r}\times\vec{f}$)
- If the angle between two vectors is $\theta$ the cross product is $\vec{f}\times\vec{r}=|\vec{f}|\,|\vec{r}|\sin\theta$ and is perpendicular to $\vec{f}$ and $\vec{r}$ with the direction determined by the right hand rule
- Calculated with $i,j,k$: If we have two vectors $\vec{p}=(p_1,\, p_2,\, p_3)$ and $\vec{q}=(q_1,\, q_2,\, q_3)$ we can associate $i,j,k$ with the first, second and third elements of a vector. The cross product is then \[\vec{p}\times\vec{q}=\left|\begin{matrix}i & j & k\\p_1& p_2& p_3\\q_1& q_2& q_3\end{matrix}\right|\]
- Calculated as a Matrix times a vector: It is possible to write a vector in Skew form (also called adjoint form) so
A skew matrix is one where $S^T=-S$ . This particular matrix has some interesting properties but in this context it allows the cross product to be written as a matrix times a vector so
\[\vec{p}\times\vec{q}=\vec{p}_\times\vec{q}=\begin{bmatrix}0 & -p_3 & p_2\\ p_3&0&-p_1\\ -p_2&p_1&0\end{bmatrix}\begin{bmatrix}q_1\\ q_2\\ q_3\end{bmatrix}\] Torque example given in Vectorintro.pdfCoordinate frames
A coordnate frame is defined by a set of basis vectors that need to be non-coplanar and are usually orthogonal.
A coordinate frame is usually asociated with an object (or vectors) and allows invariants of that object to be captured in a more convenient way
Force equivalence
Multiple forces acting on a point or pin can be replaced by a single force. This force is the vector sum of all force vectors. a force can be represented as a sum of force vectors
An unbalanced force (or vector sum of forces) will result in an acceleration. An unbalanced torque (a vector sum of torques) will results in angular acceleration.
A comment on Static and dynamic systems
- A static system only has fixed elements in a particular coordinate frame
- A dynamic system has moving elements in a particular coordinate frame. If these elements move together they can be assigned a coordinate frame
Materials (a short intro)
More details later in the course.
- What is the definition of a material?
- Is it only solids, liquids and gasses that are materials? Any others?
- Stress is defined as the force exerted over the area is this the same as pressure?
- Shear stress
- Tensile stress
- Compressive stress
- Strain is the deformation of a material in response to stress
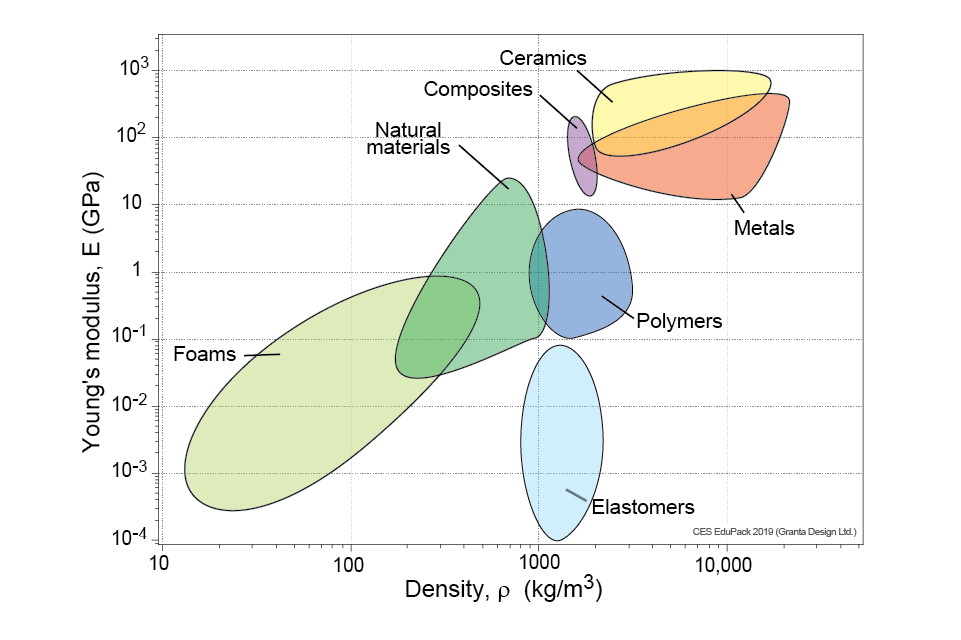
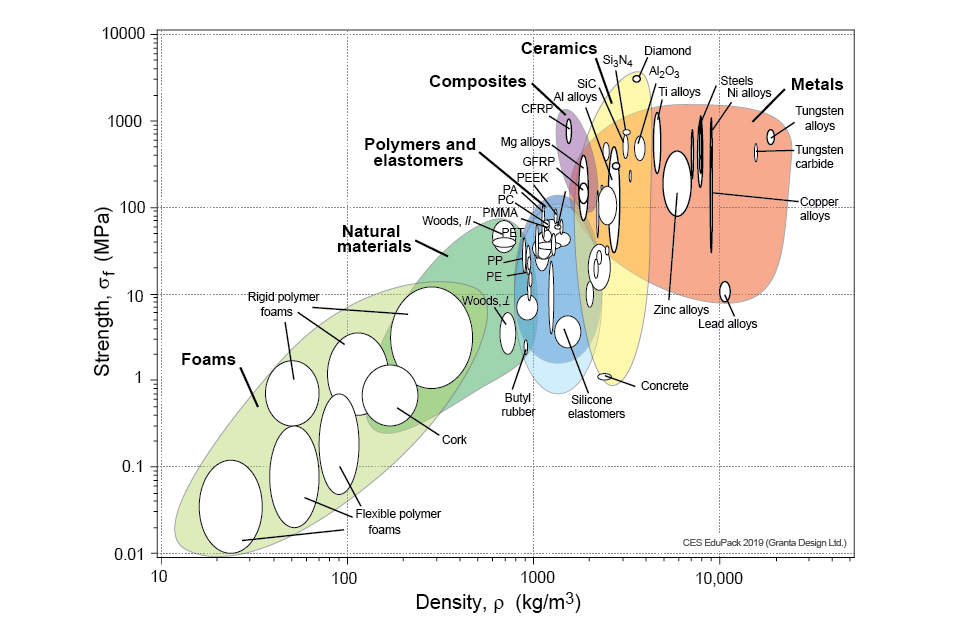
What is
- A ceramic?
- A composite?
- A metal (alloy) ?
- A foam?
- A polymer?
- An elastomer?
For the above groups, in what class would you consider the following materials
- Aluminium (dural)
- Brick
- Concrete
- Cork
- Nylon
- Polystyrene
- Steel
- Stone
- Titanium
- Wood
Can you define
- density?
- strength?
- stiffness?

Biomaterials
- List some of the materials in animals?
- Are cells responsible for all material manufacture in animals?
- Give some examples of cells that make biomaterials?
W.S. Harwin 10/10/2023